Waarom je de bezoekersverdeling van een A/B-test niet tussendoor mag aanpassen

Bij het horen van de term Simpson’s Paradox is er een grote kans dat je direct denkt aan de Tv-serie over de gele lompe goedzak met weinig herseninhoud en een continue hunkering naar Duff bier en donuts. Maar dat is helaas niet correct.

De Simpson’s Paradox verwijst naar een statistische situatie waarin er een trend of relatie wordt geobserveerd tussen verschillende groepen, die weer verdwijnt op het moment dat de groepen worden gecombineerd. Je zou het kunnen zien als een soort rekenkundige truc. Afhankelijk van hoe de groepen worden gecombineerd is de conclusie anders en soms zelfs tegengesteld.

Als web analist of data scientist is het belangrijk op de hoogte te zijn van dit fenomeen bij het analyseren van data en in het bijzonder in het licht van de bezoekers verdeling in A/B-testen.

Hoe werkt de Simpsons Paradox?

Mark Liddell heeft de Simpson’s Paradox erg duidelijk uitgelegd in de volgende Ted Education video:

Een bekend voorbeeld uit de medische wetenschap is een studie naar behandelmethodes voor nierstenen. Behandelmethode A is een normale operatie en behandelmethode B een methode waarbij slechts een kleine incisie is vereist. Opvallend in de resultaten is dat behandelmethode A voor zowel kleine (93% versus 87%) als grote nierstenen (73% versus 69%) de beste optie is, terwijl op geaggregeerd niveau behandelmethode B als beste uit de bus komt (78% versus 83%). Elke behandelmethode is 350 keer uitgevoerd.

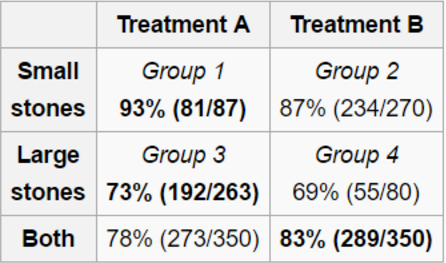
Het probleem ligt in het verschil in de verhouding van de kleine ten opzichte van de grote nierstenen tussen de twee methodes: methode A heeft 87 kleine en 263 grote nierstenen behandeld en methode B 270 kleine en 80 grote nierstenen.

Op het moment dat er één overall succespercentage wordt berekend, zal het succespercentage van behandelmethode A schuiven richting de succesratio van de grote nierstenen, terwijl bij behandelmethode B de ratio voor het grootste deel wordt bepaald door het succesvol behandelen van kleine nierstenen. Hierdoor komt behandelmethode B over het algemeen als beste uit de test.

Er zijn dus twee condities waardoor een Simpson’s Paradox kan optreden:

• wanneer de geobserveerde groepen erg uiteen liggen betreft het aantal observaties (hier: de verhouding kleine en grote nierstenen in de testgroepen) en;
• wanneer er een verborgen conditionele (zogenaamde ‘lurking’) variabele is die invloed heeft op de geobserveerde relatie (hier: de succesratio van het behandelen van kleine en grote nierstenen).

Deze twee condities zullen ervoor zorgen dat de daadwerkelijke relatie tussen verschillende groepen wordt verdoezeld.

“There are three kinds of lies: lies, damned lies, and statistics.”  — Mark Twain

Relevantie in A/B-testen

Waarom is kennis van de Simpson’s Paradox belangrijk in het licht van A/B-testen? Met name, omdat deze paradox het antwoord geeft op de vraag: “mag ik tijdens de A/B-test de bezoekers verdeling aanpassen als één variant duidelijk beter presteert dan de andere?”. Het antwoord luidt: Nee! Onderstaand voorbeeld laat zien, waarom dit geen goed idee is.

Tijd voor een voorbeeld

Stel dat je een A/B-test start vlak voor het weekend en je verdeelt het verkeer netjes 50/50 – iedere variant krijgt 2.000 bezoekers per dag. Na het weekend bekijk je de eerste resultaten en ziet dat B al twee dagen een stuk beter presteert dan A.

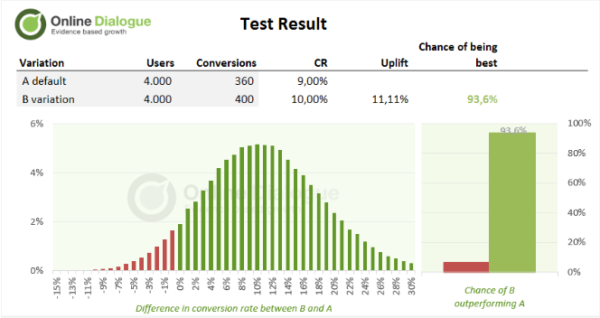
Het conversiepercentage van variant B ligt 11,11% hoger dan dat van A. Een Bayesiaanse calculatie laat zelfs zien dat de kans dat B beter is dan A 93,6% is.

Hierop besluit je de bezoekers verdeling van de test aan te passen naar 10/90: vanaf maandag krijgt 10% van het bezoek variant A te zien en 90% de beter presterende variant B. Je houdt de statistieken nauwlettend in de gaten en ziet tot je tevredenheid dat B het beter blijft doen dan A (alhoewel het verschil minder groot wordt). Wanneer de test een volle week heeft gedraaid eindigt de test en maak je de balans op.

En wat blijkt: op totaalniveau presteert variant A beter dan variant B! Variant A heeft een uiteindelijk conversiepercentage van 8,7% en variant B van 8,6%.

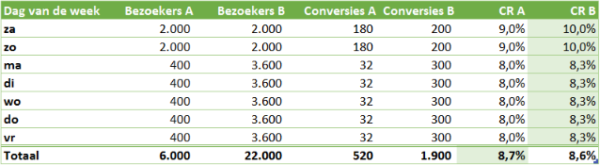
Hier zie je de Simpsons Paradox vol in werking: op elke afzonderlijke dag presteert variant B beter dan A, maar de groepen gecombineerd laat een ander beeld zien. Dit wordt veroorzaakt doordat de groepen ongelijk verdeeld zijn én er eenderde variabele invloed heeft op de conversie (dag van de week). Doordeweeks liggen de conversiepercentages lager dan in het weekend en de verschillen tussen A en B zijn dan ook minder groot.

Concluderend, tijdens de duur van de A/B-test mag je de bezoekers verdeling niet aanpassen. Al zou je geen dag van de week effecten hebben, dan nog is dit geen goed idee. Er kunnen altijd andere derde variabelen aan het werk zijn (bijvoorbeeld uur van de dag, verkeersbron of device).

Daarbij komt ook nog eens dat indien de traffic split wordt aangepast dit enkel effect heeft op nieuwe bezoekers. Hierdoor worden terugkerende bezoekers over- of ondervertegenwoordigd in één van de groepen als een A/B-test wordt afgerekend op unieke bezoekers (immers, zij behouden hun originele variant).

Is er een remedie?

Wat belangrijk is om in ogenschouw te nemen is dat de Simpson’s Paradox enkel opduikt als de sampling niet uniform is. Of te wel, wanneer de steekproefgrootte van de segmenten ongelijk is. Dit probleem kun je te lijf gaan door te zorgen dat segmenten random worden verdeeld over de varianten (en de aantallen per segment groot genoeg zijn om valide uitspraken over te doen). Doorgaans gaat het randomiseren wel goed, maar om extra zekerheid in te bouwen zou je een gestratificeerde steekproef kunnen gebruiken. Een gestratificeerde steekproef is het opsplitsen van een populatie in homogene wederzijds uitsluitende subgroepen, waaruit je vervolgens random samples trekt. Echter, de A/B-test tools op de markt kunnen hier nog niet mee uit de voeten.

Tot slot, wees altijd kritisch in het trekken van conclusies. Segmenteer de geaggregeerde data op betekenisvolle dimensies (indien random verdeeld) en bepaal of de conclusie hout snijdt. Vind je per segment toch een tegenovergesteld effect, herhaal de test dan nogmaals in een nieuwe speciaal getargete A/B-test om de bevindingen te valideren.